Digital 1 : Number Systems
우리가 익숙한 수체계는 10진법이며
그 각각의 요소에 대해 coefficient와 base라고 부른다.

10진수 144를 2진수로 변환하세요 = 10010000(2)

10 넘어가면 10, 11, 12, 13, 14, 15 대신 A, B, C, D, E, F 쓴다.
2진수 체계와 16진수 체계가 가장 많이 쓰인다.

110011 을 10진수로 변환하세요 = 51(10)
110011 을 16진수로 변환하세요 = 44(16)
1보다 작은 경우에는 다음과 같은 방식으로 처리함.
0.6875(10) = 1101(2)


하지만 우리가 Unsigned 수체계에서 배웠는데
Signed 체계로 넘어가야 양수와 음수를 둘다 다룰 수 있음.
Signed 체계에는 보수가 존재하고. 보수에는 1의보수와 2의보수가 존재.

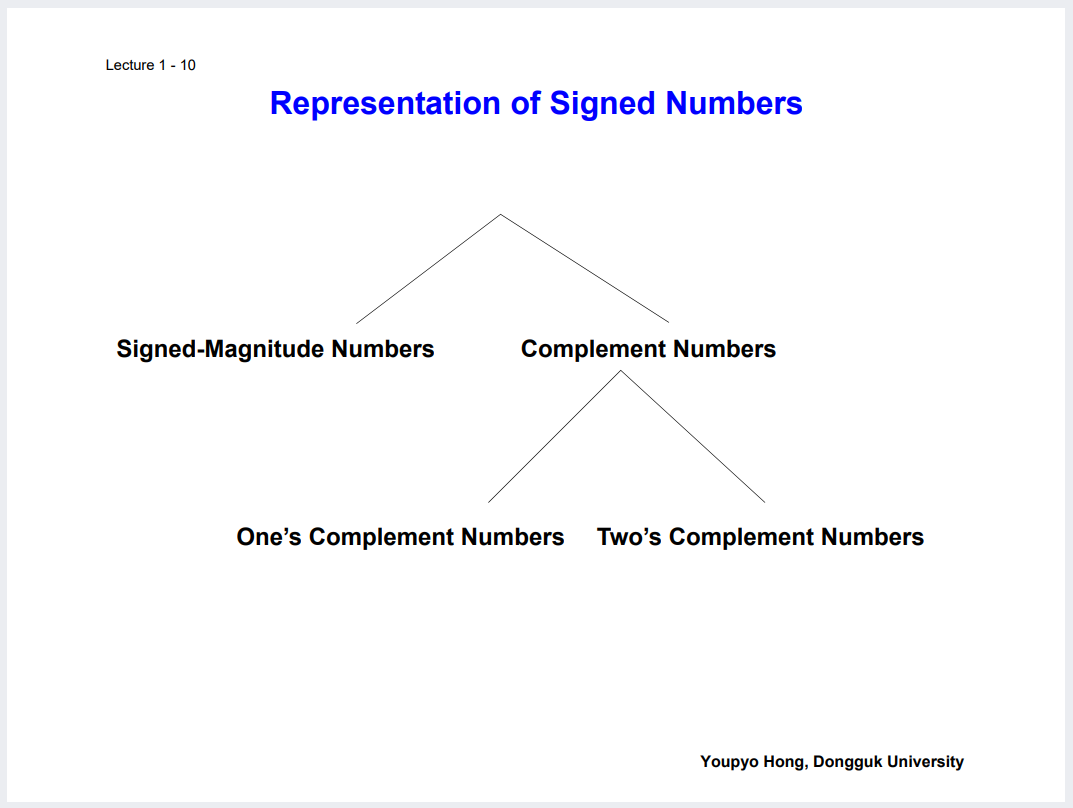
Signed 가장 앞자리 MSB를 이용해서 양음을 표현함.
하지만 덧셈뺄셈 연산할 때는 보수체계를 이용해줘야 함.


그래서. 연산을 어떻게 하느냐. (부호있는 자료형의 비트연산)
더하는건 더한다음에 오버플로우 sign에 대해서 버리면 된다.
하지만 빼는 것은 음수를 two's complement 처리해준다음 더해주면 됨.


하지만 오버플로우 나는 문제에 대해서는 생각을 해야하는데
(한정된 메모리를 사용하고 있다고 생각해보면)
같은 부호의 수를 더하거나, 다른 부호의 수를 더할때 발생할 수 있으며
다른 부호의 수를 더하거나, 같은 부호의 수를 뺄때는 발생하지 않는단 특징있다.
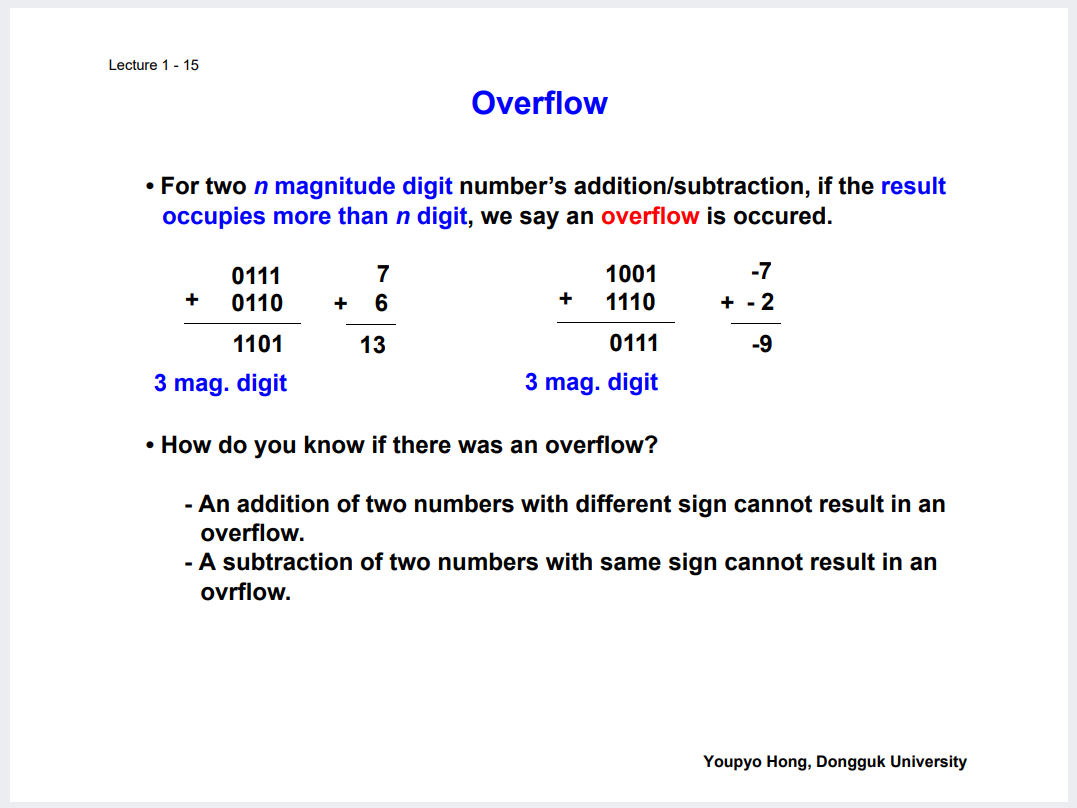
Carry into the sign-bit 와 Carry out of the sign-bit 가 다른 것을 보고, Overflow 판별이 가능하다.
그래서 판별이 된 경우, 앞에 0000이 있다고 간주하거나, 1111이 있다고 간주하는 것으로 해결가능하다.


Digital 2 : Codes
코드에 대해 배울거고, BCD Codes, Excess Codes, Gray Codes, Alphanumeric Codes, ASCII Codes 등이 있다.
BCD Code는 10진수를 2진수처럼 나타내는 것이다. 그래서 0부터 9까지만 표현한다.

이런 특징이 있기 때문에, 2진수 또는 10진수처럼 그냥 연산할 수 없다.
10까지는 괜찮은데, 11부터는 표현이 안되기 때문.
그래서 이것 또한 마찬가지로 오버플로우 발생이 판단된 경우
6(0110)을 더해주거나, 10(?)을 빼주는 방법으로 진행할 수 있다.
(이 부분 지금 이해가 안되는데, 우선 지금 중요한건 아닌 것 같아서 패스)

Excess-3 코드는 BCD에서 3(0011)을 더한 체계이다.
그때 Input Output & Don't use에 따라 다음과 같이 카르노맵 표현이 가능하다.
https://dad-rock.tistory.com/385
[Digital Logic] BCD to Excess-3 Conversion Circuit | BCD에서 3-초과 부호로 변환하는 회로
BCD to Excess-3 Conversion Circuit BCD에서 3-초과 부호로 변환하는 회로 * BCD Code (URL) * Excess-3 Code (URL) : BCD 코드에 0011을 더한 코드 체계이다. Specification Inputs: 4 Variables (\(A, B, C, D\..
dad-rock.tistory.com

GreyCode는 연속되는 수간에 비트가 하나씩만 다른 특징을 가지며
가중치가 없기 때문에 연산에는 부적합하고, 전송에 적합한 성질 갖는다.

https://ko.wikipedia.org/wiki/%EA%B7%B8%EB%A0%88%EC%9D%B4_%EB%B6%80%ED%98%B8
그레이 부호 - 위키백과, 우리 모두의 백과사전
ko.wikipedia.org
Alphanumeric Code와 ASCII Code는 알파벳 등 characters를 binary으로 표현하기 위한 목적을 갖는다.

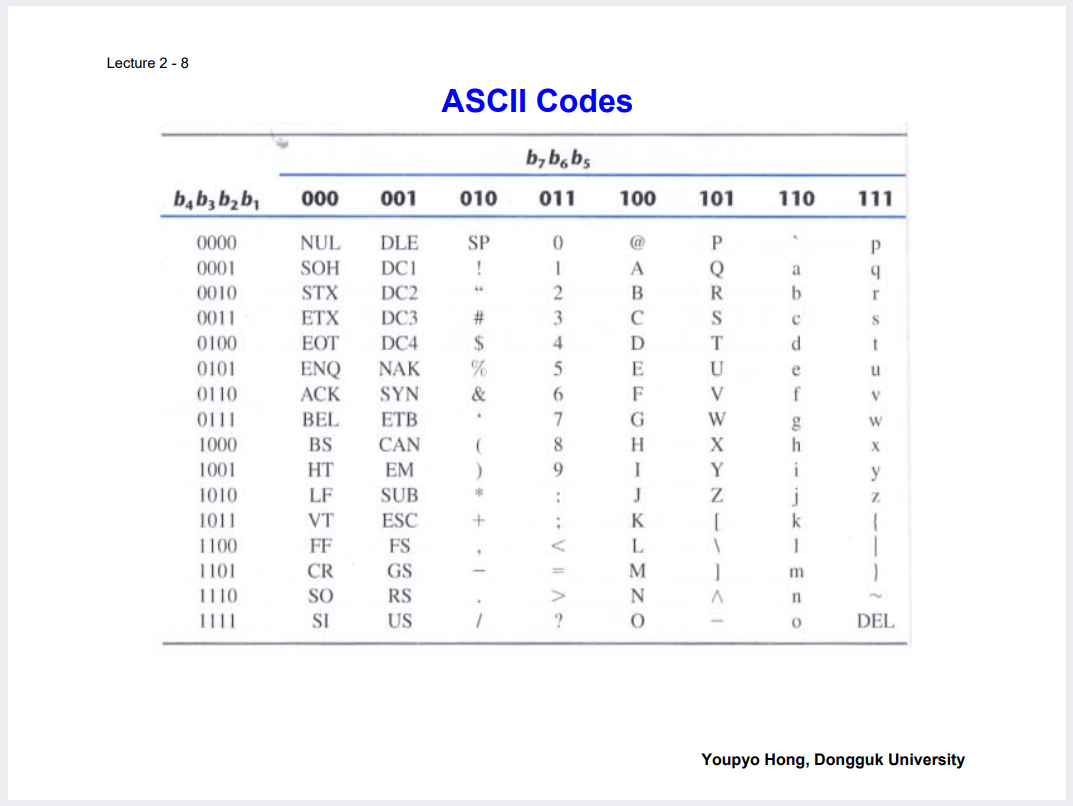
많은 컴퓨터들은 8비트 즉 1바이트를 기본 data unit으로 사용한다.
그래서 ASCII 같은 경우는 남겨둔 1자리를 Parity bit로 검증용으로 쓴다.


Digital 3 : Logic and Gates
주요 로직은 AND, OR, NOT 이 기본적으로 있다.

그리고 그 연산의 결과(발생가능한 조합)는 Truth Tables에 따라 표현이 가능하다.

그 로직을 회로에서 가능케하는 것이 게이트이다.

게이트는 단순히 2개의 Input만 가능한 것이 아니라 1개 또는 다수개의 Input을 가질 수 있다.
AND는 한개라도 1이 있으면, 결과는 항상 1이며
OR는 모든것이 1일때만, 1을 만든다.

이러한 집적회로는 반도체적 물성을 함께 고려할 수는 있다.

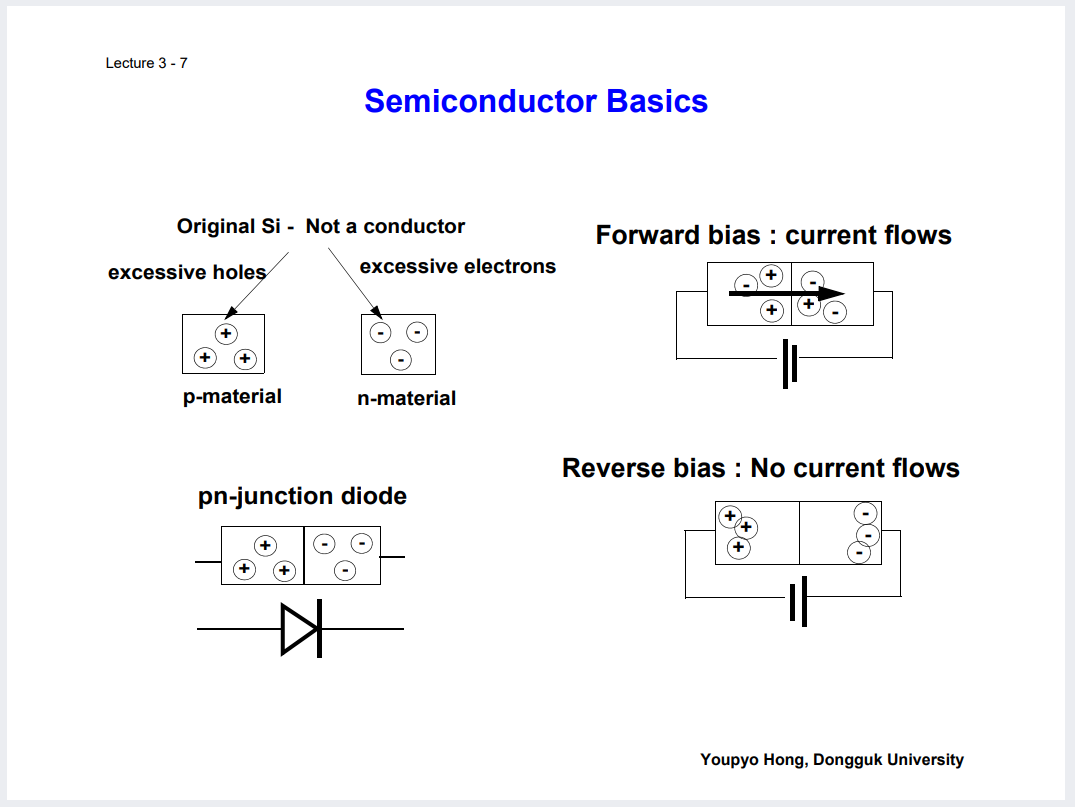
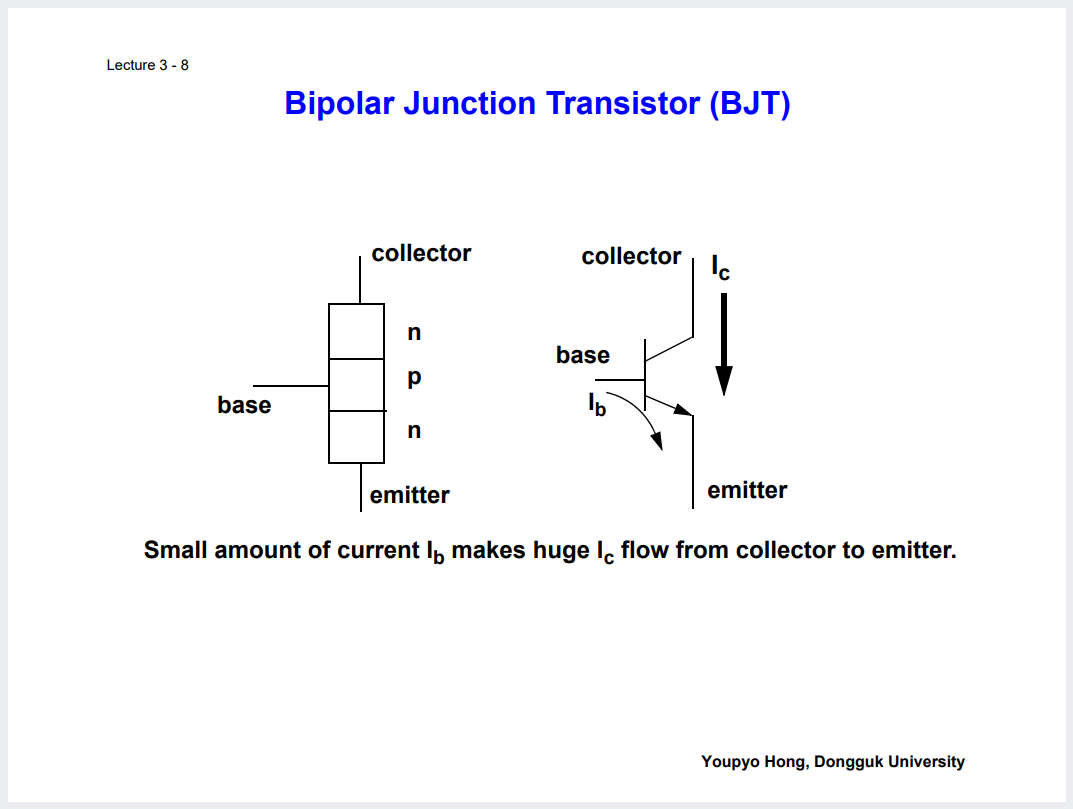
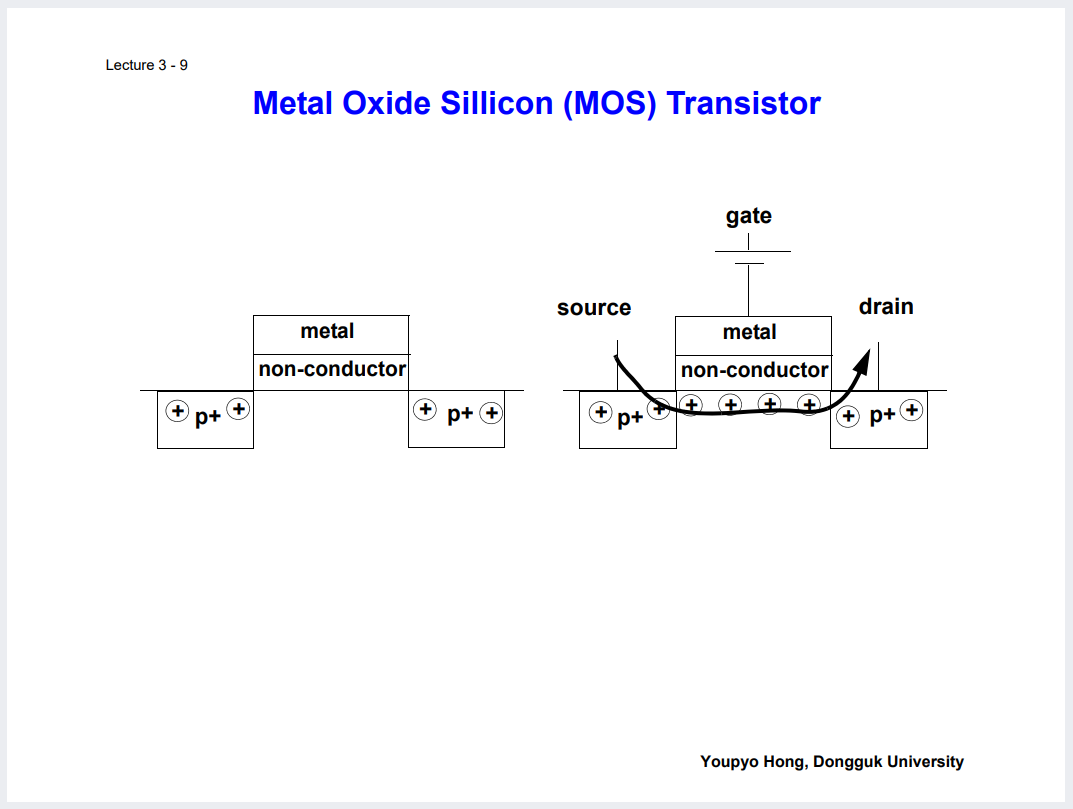

그래서 이러한 반도체적 특성을 고려하면
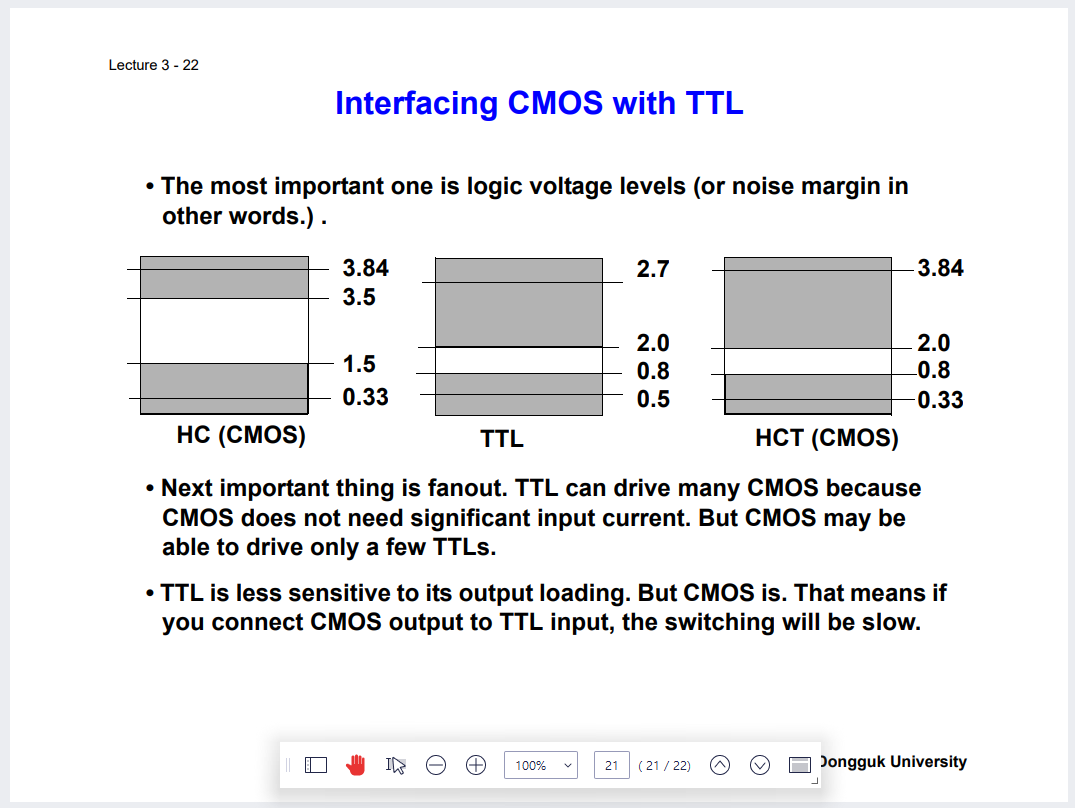
Logic Voltage Level 같은 개념이 존재하기는 함. 역치에 해당하는 것.

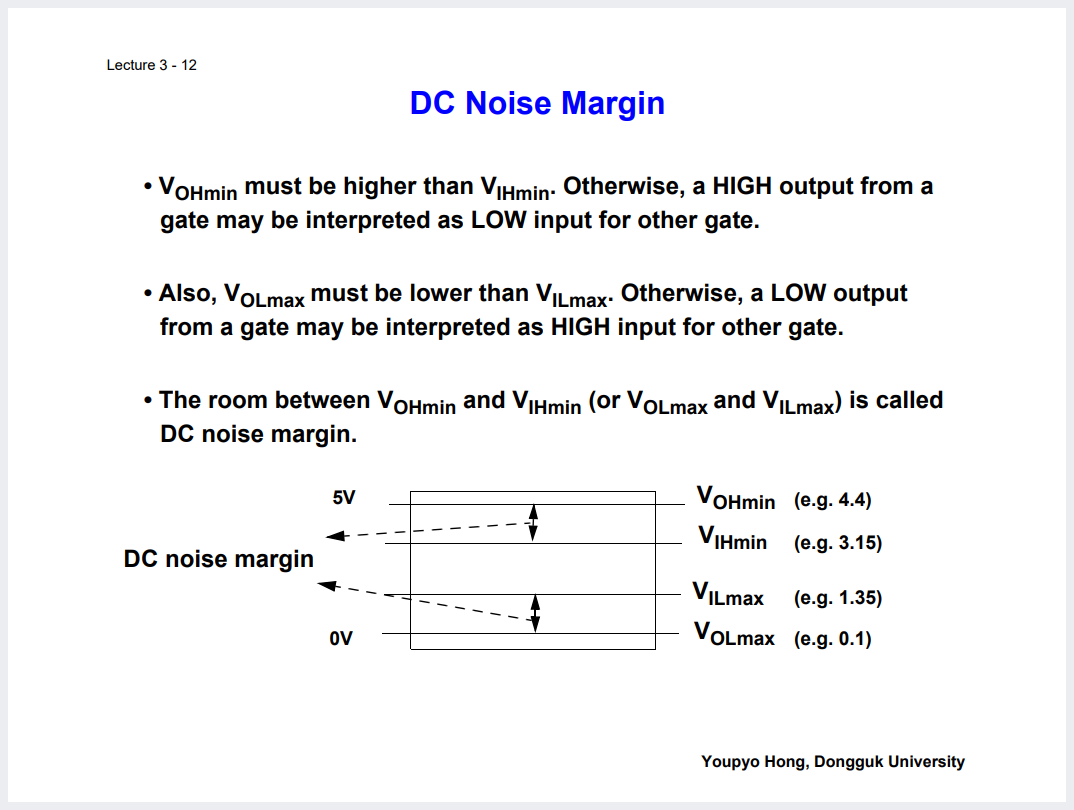

이 성질들을 이용해서 우리는 다음과 같은 개념을 고려해야한다.
Fanout
하나의 소자에 너무 많은 핀을 연결하면 오작동의 원인이 된다.

하나의 게이트를 통과하는데 그 전후시간에 약간의 Transition Time이 붙는다.
이건 하나의 신호 내에서의 V_IHmin 과 V_ILmax 간의 역치를 넘기 위한 작은 시간.
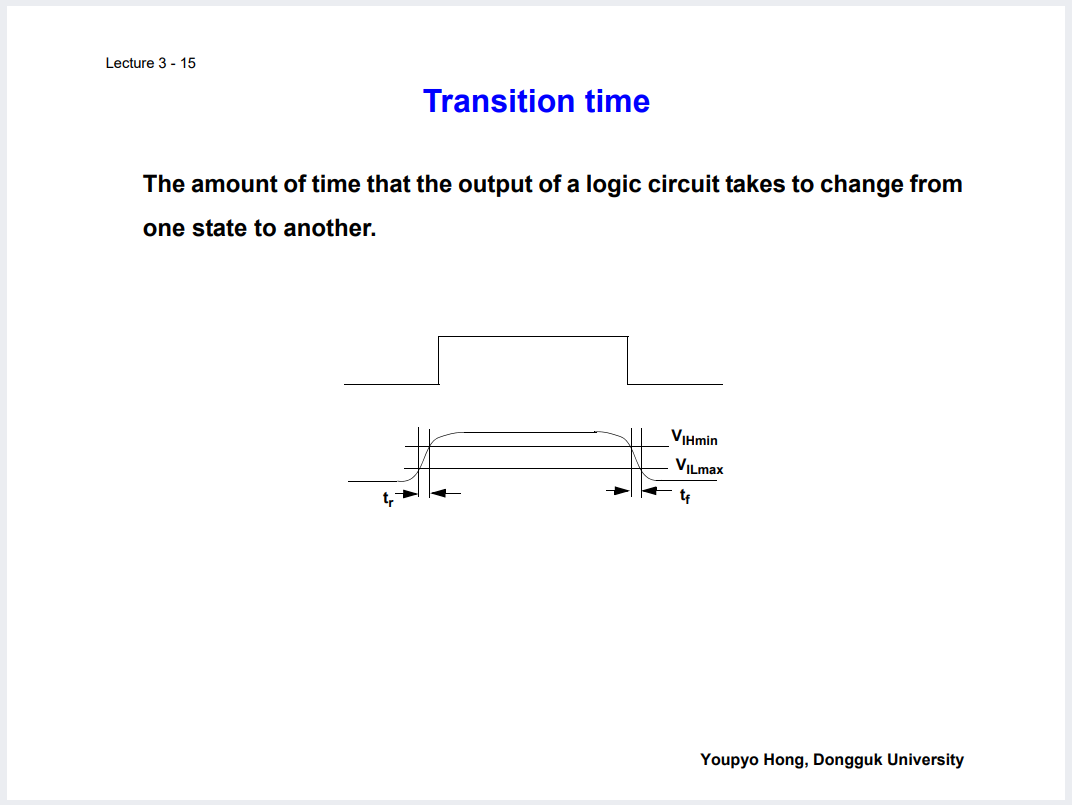
통과하는데 걸리는시간에 조금 더 가까운 것은 Propagation Delay 이다. Input에서 Output 까지의 시간갭.
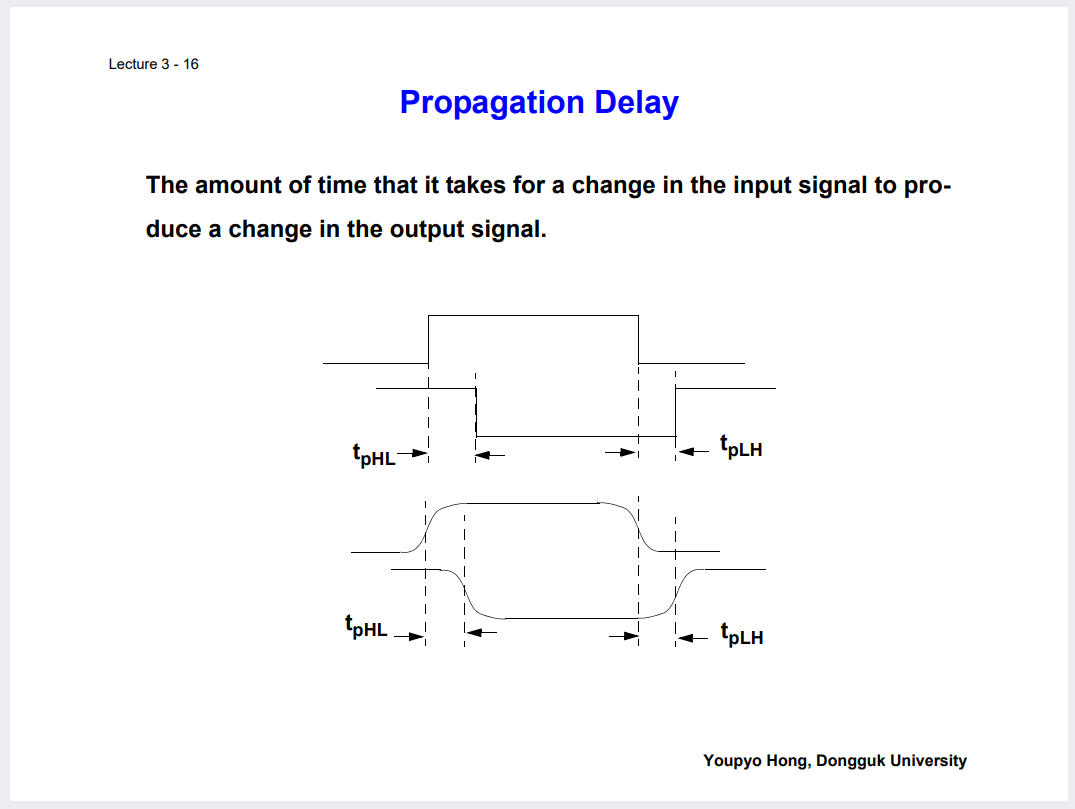
무언가의 Output Transition을 만들기 위해, 또는 만들지 않더라도 유지해주고 있기 위해 들어가는 전압소비가 있다.

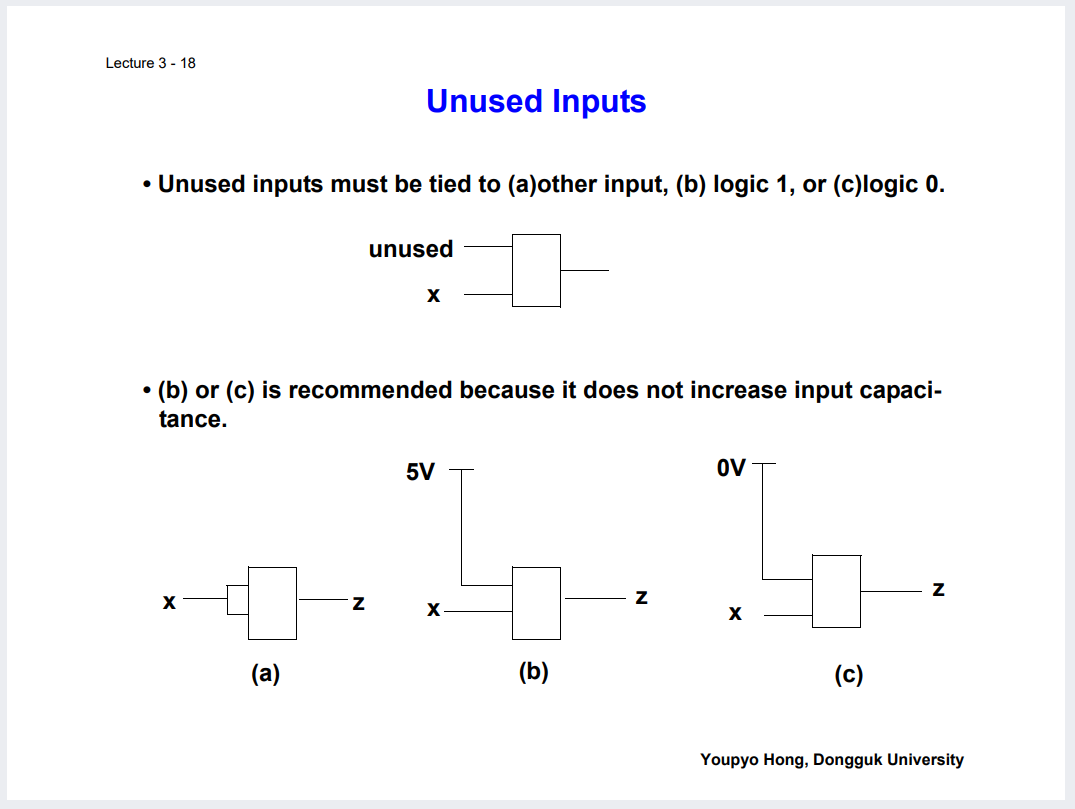
안쓰는 핀이더라도, 오류를 방지하기 위해 5V 또는 0V (1 또는 0)에 값을 물려주어야 한다.
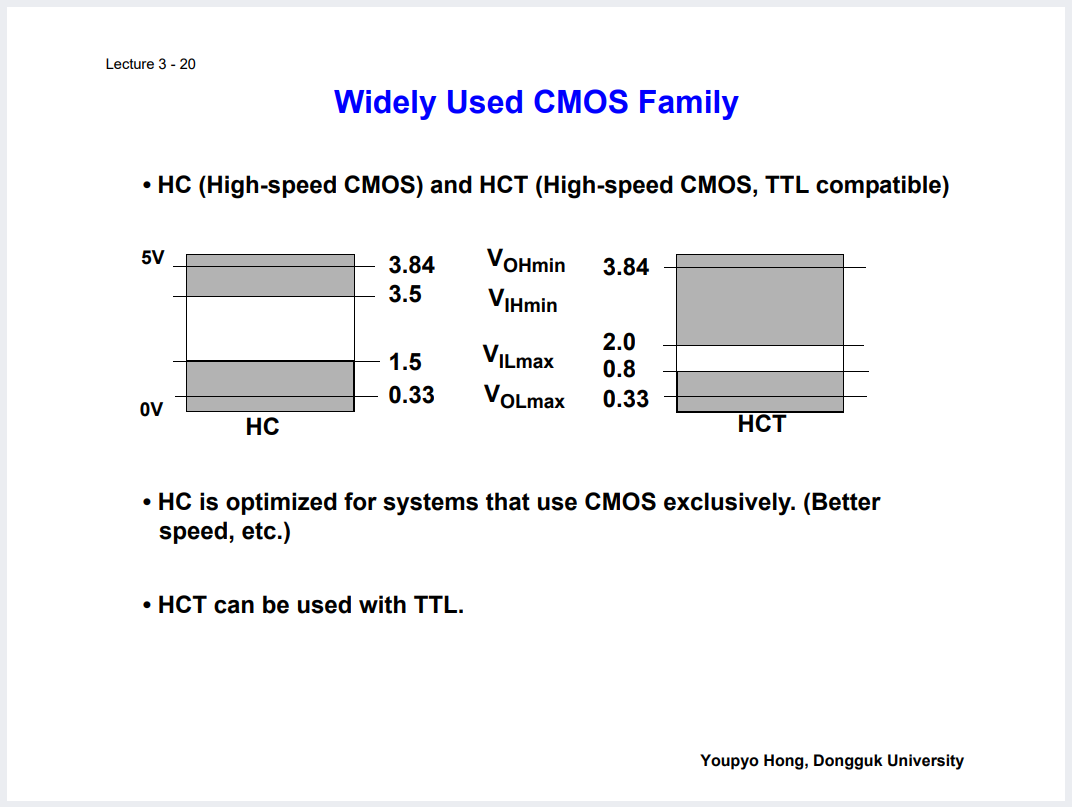
소자의 Naming Convention 들이 존재한다.

MOS 중에는 CMOS와 PMOS가 있는데,
사실 압도적으로 많이 사용되는건 CMOS 계열이다.

짧게, 쇼트키 다이오드에 대해서.
쇼트키 다이오드란 무엇이고 어떤 역할을 하는 것일까?
스뮈칭 모드 파워 서플라이(SMPS)의 회로도를 보면 2차단에 쇼트키 다이오드라는 생소한 부품이 나타나 당황하게 만듭니다. 다이오드에 대해 이해 했는데 쇼트키 다이오드가 나오니 머리가 아파
mon.futurepia.com
'Engineering(SoC Design) > 디지털공학&논리회로설계' 카테고리의 다른 글
| 논리회로설계 (복습 10~12) (0) | 2022.03.11 |
|---|---|
| 논리회로설계 (복습 6~9) (0) | 2022.03.11 |
| 논리회로설계 (복습 2~5) (0) | 2022.03.11 |
| 디지털공학 (복습 8~10) (0) | 2022.03.11 |
| 디지털공학 (복습 4~7) (0) | 2022.03.11 |