Lecture4 : Switching Algebra
논리연산들이 갖는 기본적인 성질. 이건 외우고 있어야 함.

교환 결합 분배는 성립한다.

이러한 성질을 이용해 연산을 다음과 같이 함축할 수 있다.
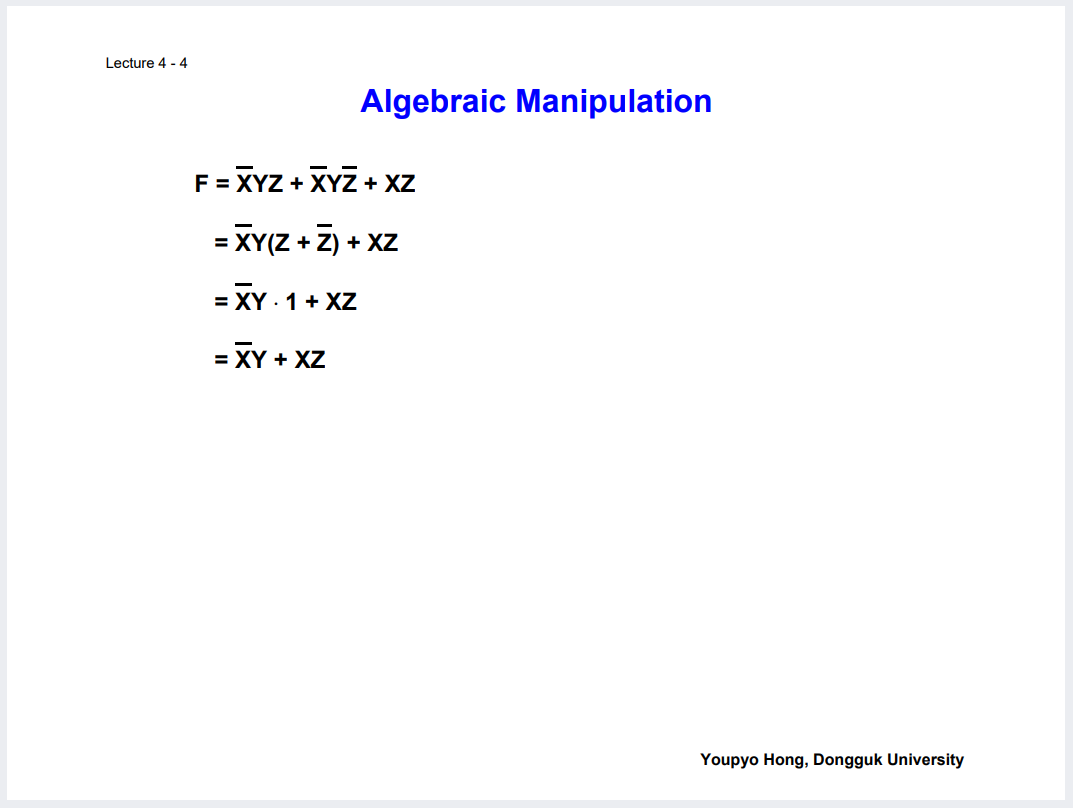
AND OR NOT 말고도 NAND 와 NOR도 존재한다.

이러한 NOT이 결합된 두 회로를 사용하면, 드모르간 법칙이 성립한다.

이 드모르간 성질은 기하적으로 공굴리기(?!)로 묘사될 수 있다.

AND OR로 이용된 그림은 NAND NOR 만으로도 그릴 수 있다. 뭐 인버터는 당연하고.


듀얼리티는 뭐였더라 기억이 안나네. (잠깐 패스하고 증명할때 살펴보자. ㅇㅋ 확인됨.)
듀얼을 취하는 것은, 양음관계와 괄호관계를 유의해서 뒤집어주면 됨. 명제가 참이면 듀얼도 참.

그래서 위에서 배운 성질들을 이용해. 다음 3가지를 증명할 수 있음.
이 부분은 직접 line by line으로 어떤 성질이 적용되고 왜 하는지 생각해보자.



Lecture5 : Karnaugh-Map
카르노맵은 집합과 여집합의 관계를 표형태로 표현해낸다는 개념이 기저. 즉 MECE하다.


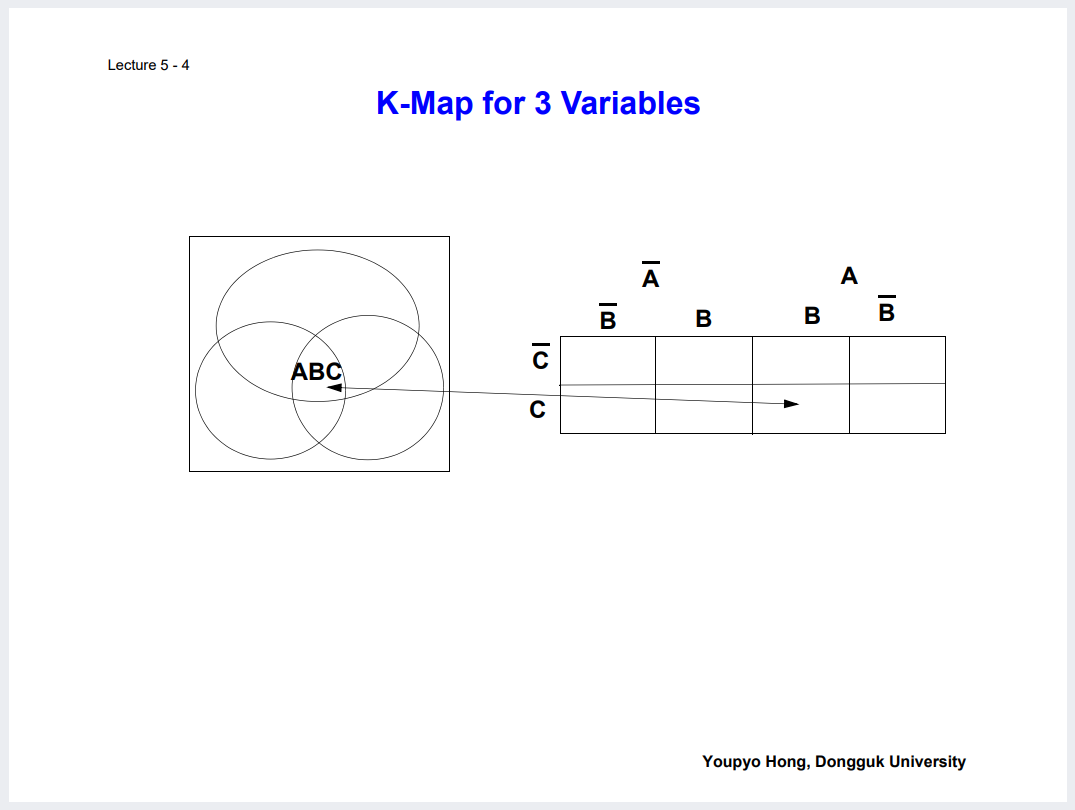
각각의 이름 구분하자. Logic Expression, Truth Table, K-Map, Logic Diagram

하나의 로직에 대해 여러가지 회로가 존재가능
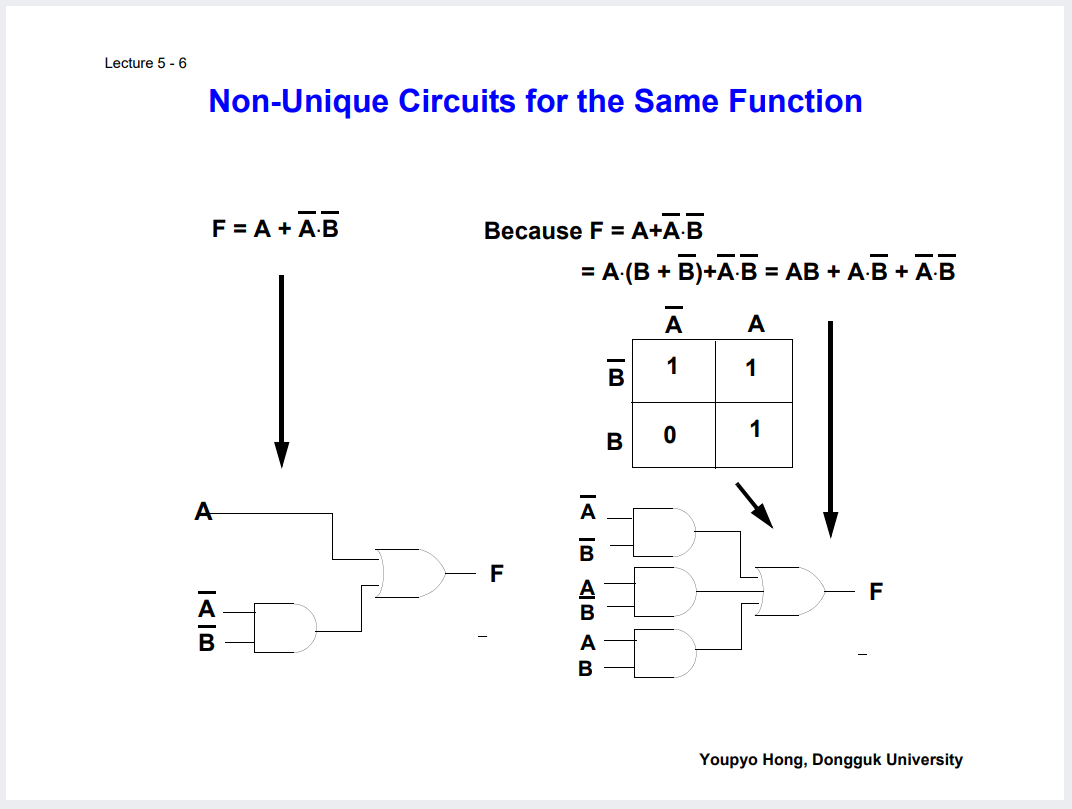
용어 정리하고 가자.

Logical Expression에 SOP같은게 있으면 Minterm으로 축소한뒤 Truth Table 그린다.

인접하게 이렇게 그리는게 표준이라고 생각
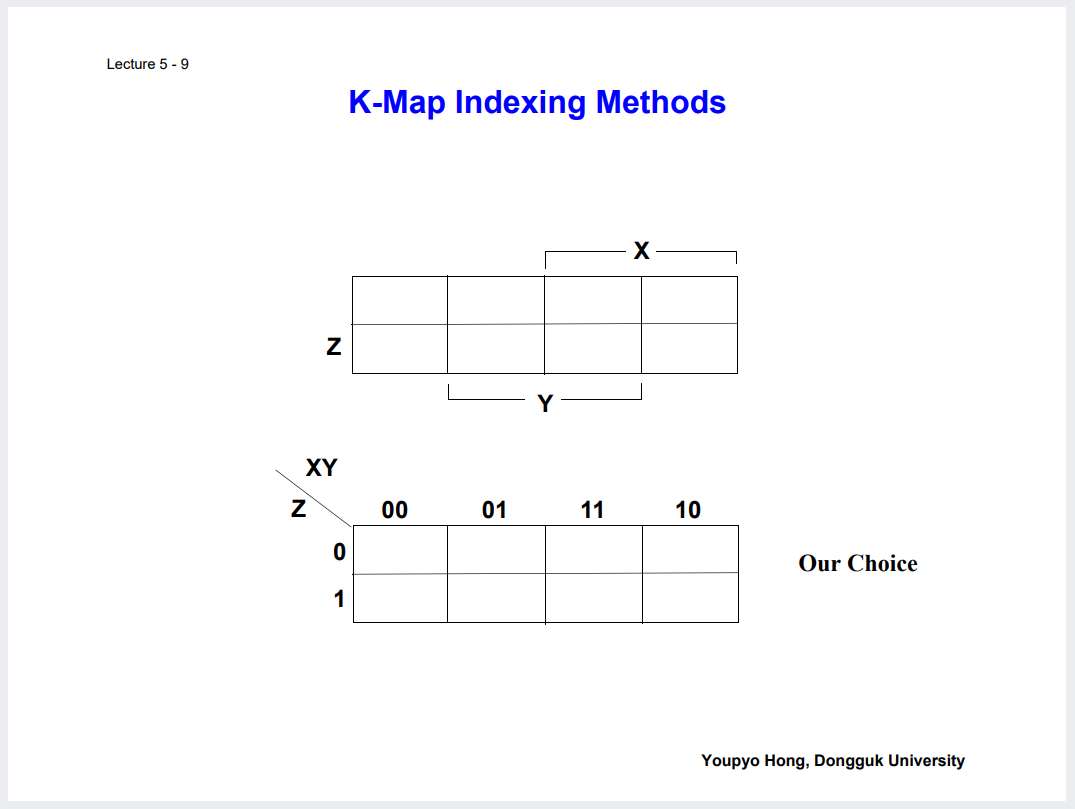
카르노맵의 성질들.
및 그러한 성질을 이용해 인접항들끼리 묶어 단순화 최소 표현 하는 것 등.




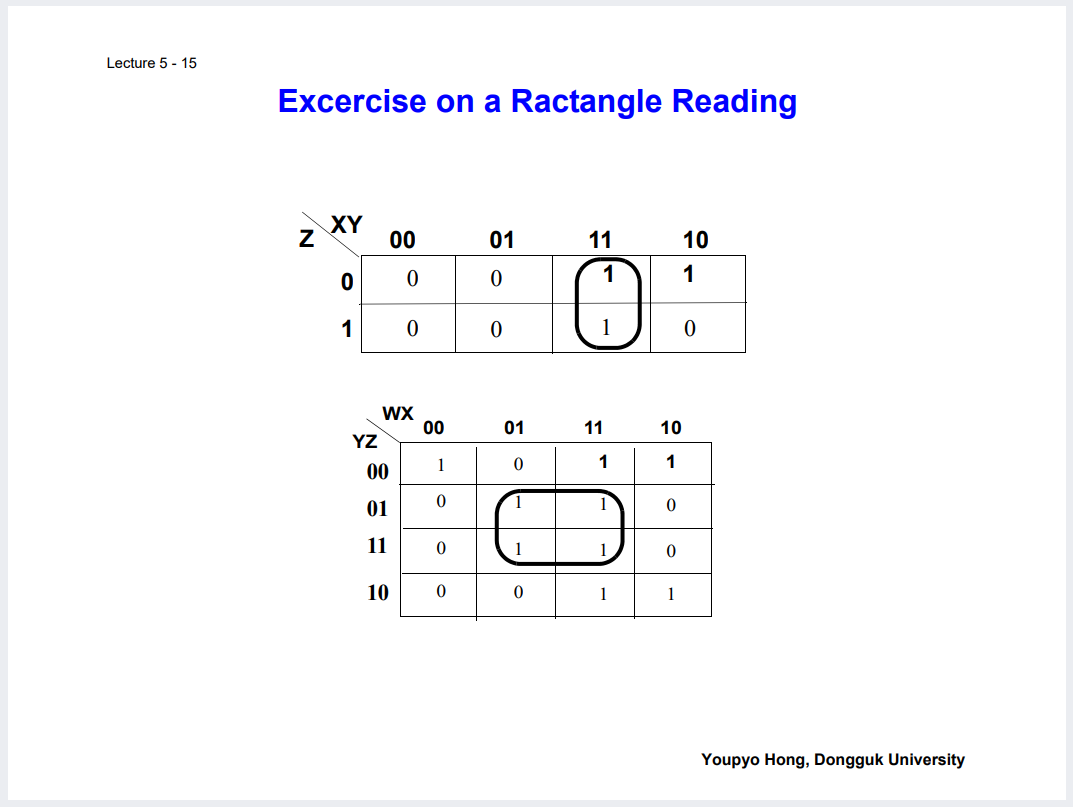

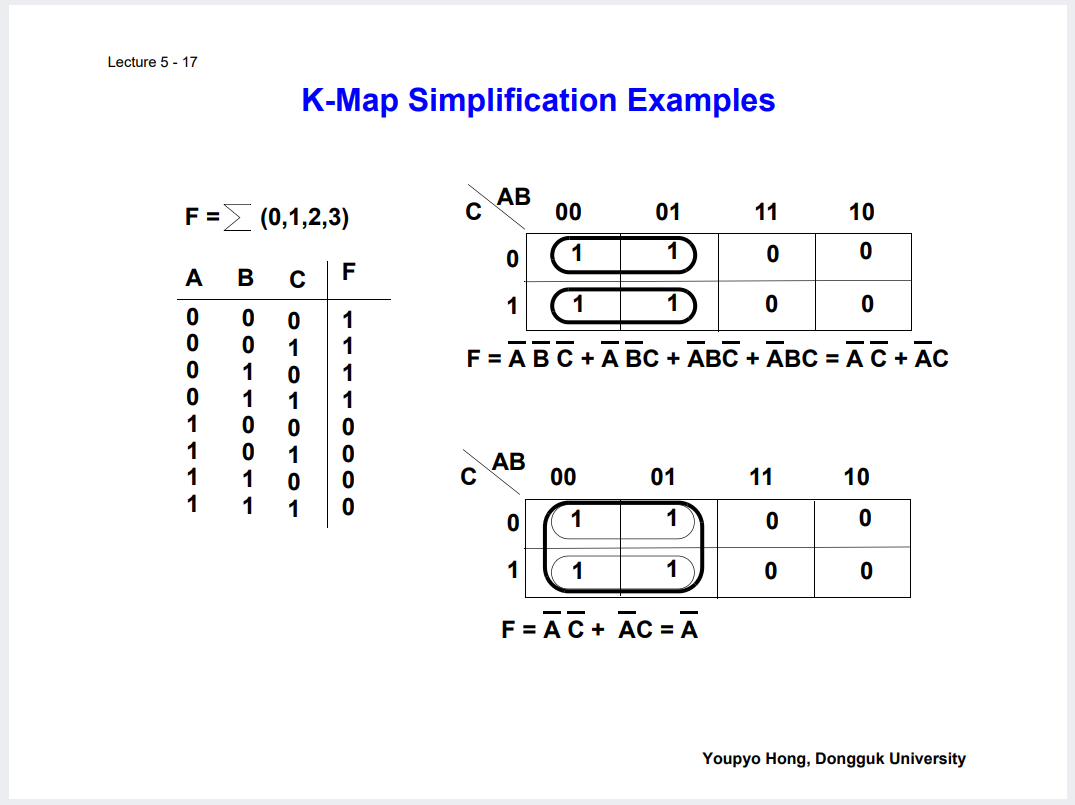
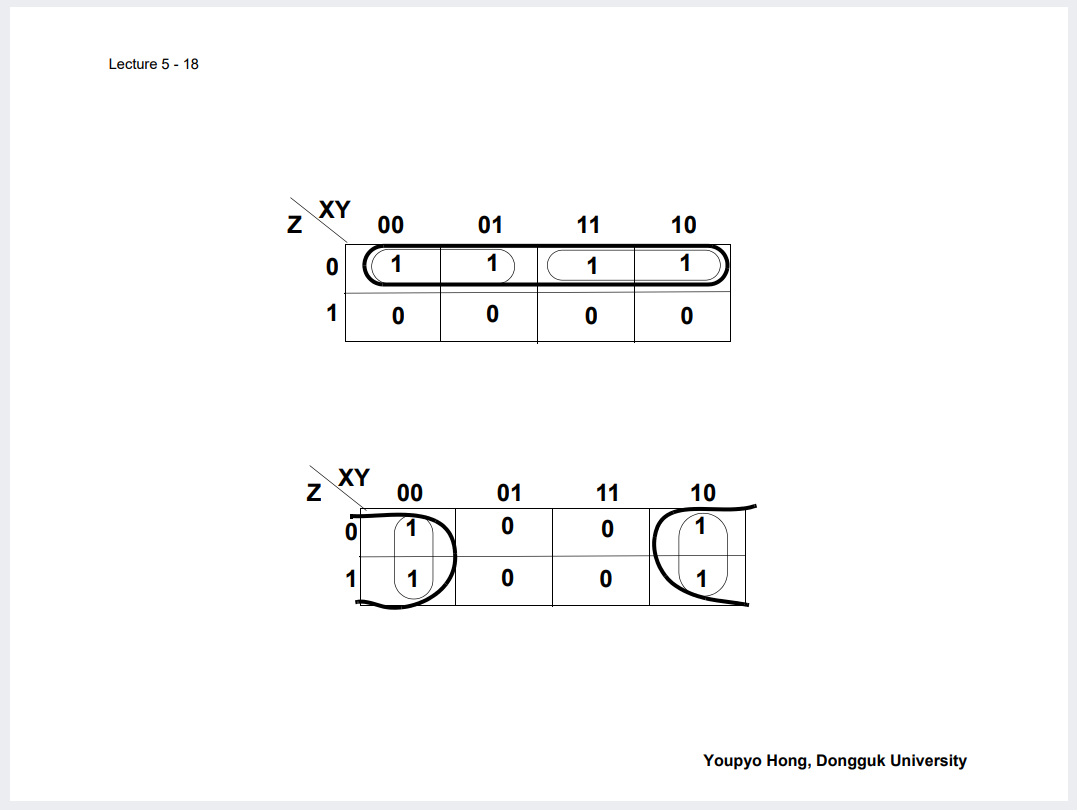
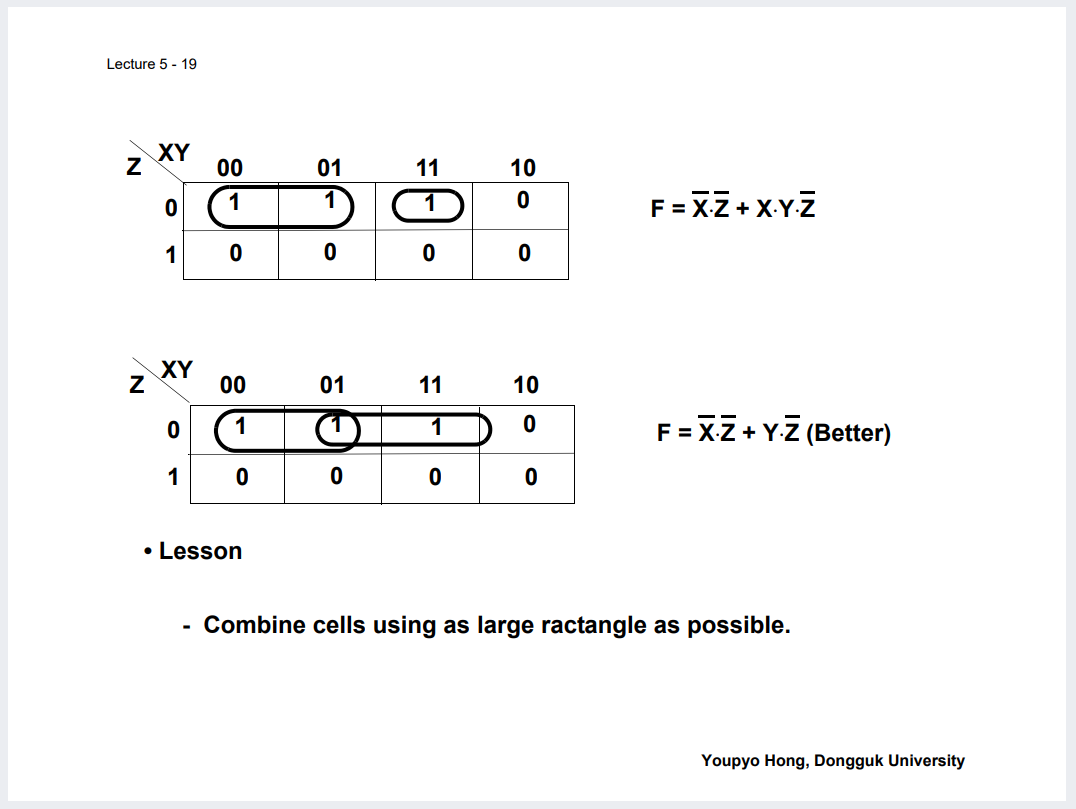

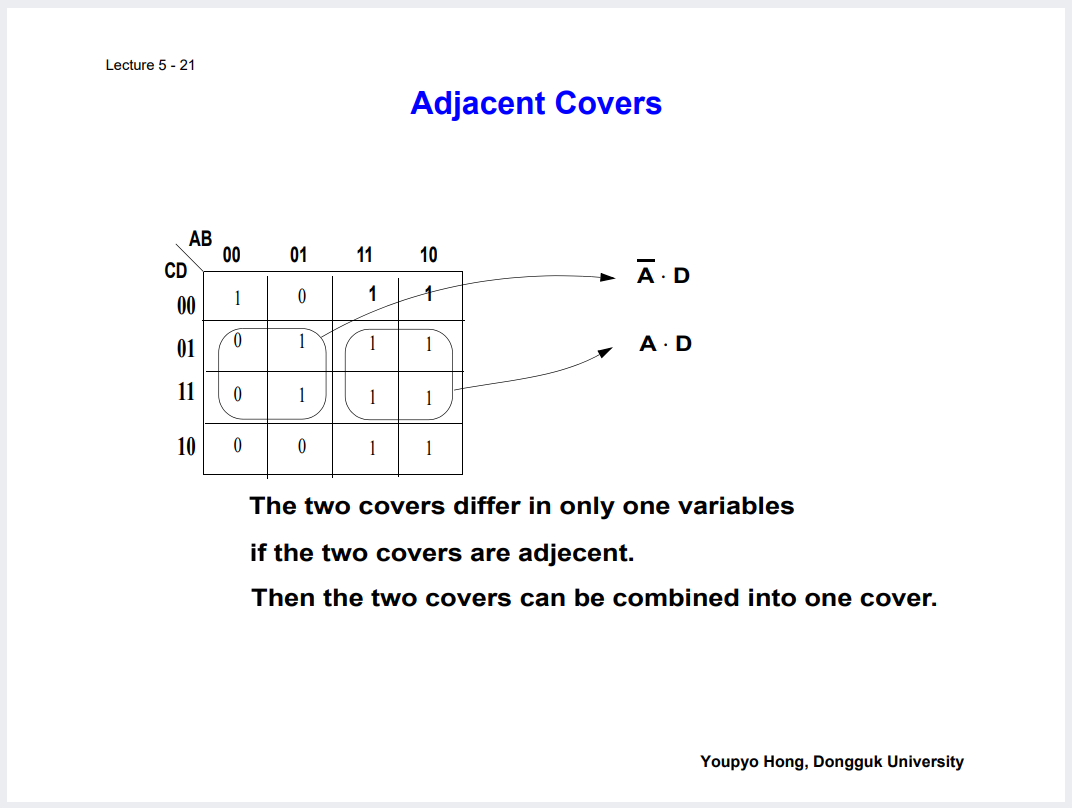



아래 예시로 직접 그리며 Practice 해보기

Lecture6 : Optimal Karnaugh-Map Simplication
카르노맵은 어느정도 다 기억나는군. Prime Implicant 찾아서, 순서대로 접근하는 방법론.
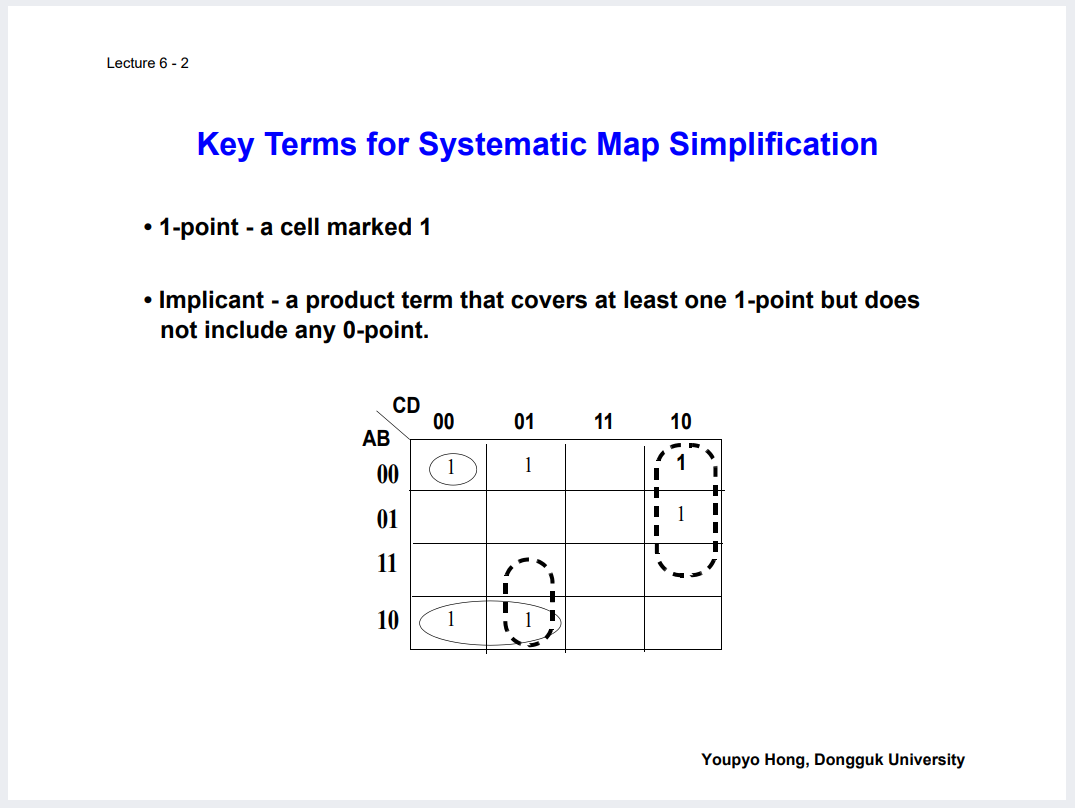



그래서, 그러나, Optimal SOP를 찾기 위해서는 하나가 결정된다기보다는 OR 꼴로 존재할 수 있음.

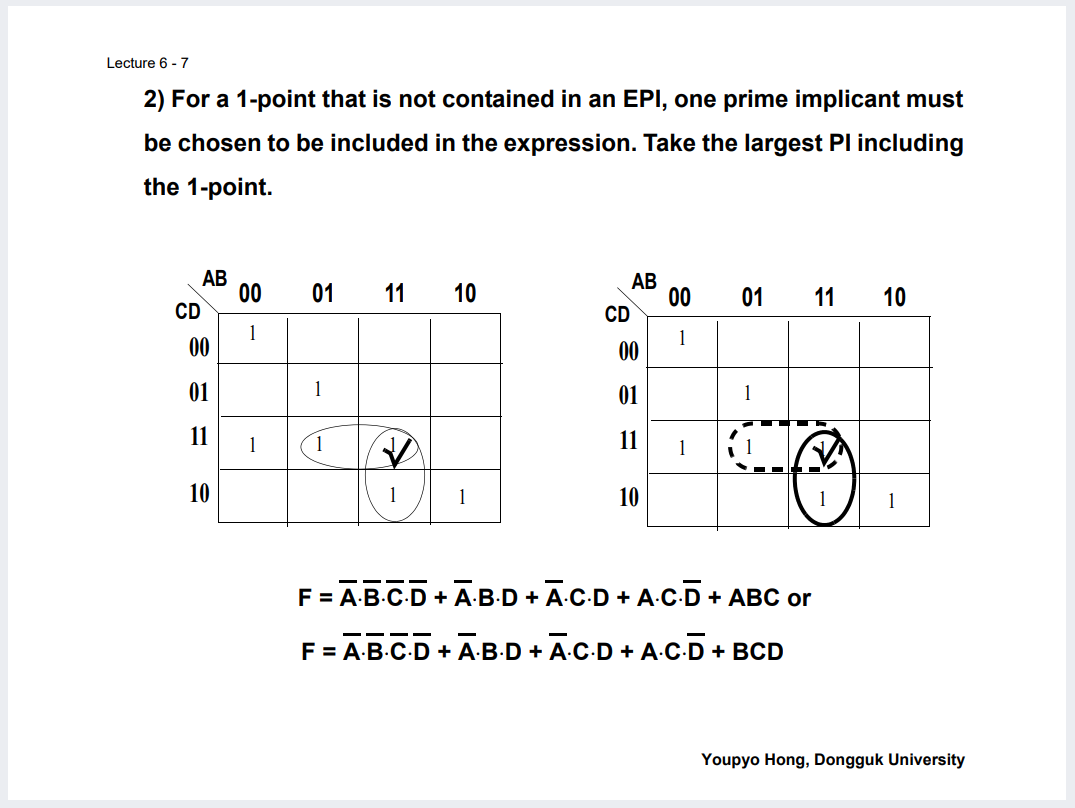

Lecture7 : Miscellaneous on Karnaugh-Map
SOP와 POS는 Complement 관계를 통해 변환시킬 수 있다.


don't care input conditions 라는 것도 존재한다.
그래서 그것은 0 또는 1 중 유리한 것으로 간주해도 괜찮다.




5변수를 이용하는 상황도 꽤 많이 나온다.

'Engineering(SoC Design) > 디지털공학&논리회로설계' 카테고리의 다른 글
| 논리회로설계 (복습 10~12) (0) | 2022.03.11 |
|---|---|
| 논리회로설계 (복습 6~9) (0) | 2022.03.11 |
| 논리회로설계 (복습 2~5) (0) | 2022.03.11 |
| 디지털공학 (복습 8~10) (0) | 2022.03.11 |
| 디지털공학 (복습 1~3) (0) | 2022.03.11 |